Intro to Numerical Systems in Computer
We use numbers every day, but how do computers understand and store information? Enter the fascinating world of binary (0s and 1s), decimal (our familiar 0-9 system), and hexadecimal (a blend of numbers and letters). Unravel the secrets of computer communication and gain a deeper appreciation for how these languages power the digital world!
- Binary (base-2):
- The core language of computers uses just 0s and 1s. This aligns with the on/off states of electronic circuits, making it fundamental for hardware.
- Decimal (base-10):
- Our everyday number system (0-9), is used for everyday calculations, currency, and counting objects.
- Hexadecimal (base-16):
- A shorthand for binary, using digits 0-9 and letters A-F (representing 10-15). This makes long binary strings more human-readable, like web color codes (#FF0000 for red).
Understanding these systems is your key to unlocking more complex concepts in computing. Think IP address conversion or data encoding – each system plays a crucial role in the digital world. By learning these “languages,” you’ll gain a deeper appreciation for how computers work their magic behind the scenes.
Decimal, Binary, and Hexadecimal Table
This table (Source: Educative) shows the equivalent values in decimal (our everyday numbers), binary (computer language using 0s and 1s), and hexadecimal (shorthand for binary) for numbers from 0 to 15.
| Decimal | Binary | Hexadecimal |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Numerical Conversion
Decimal to Binary process
A step-by-step breakdown on converting 10 to binary:
- Divide by 2, and write the remainder (0 or 1)
- Repeat the division until you reach 0
- Read the remainder column from bottom to top
| Operation | Calculation | Result | Remainder |
|---|---|---|---|
| 10 / 2 | 5 | 5 | 0 |
| 5 / 2 | 2.5 | 2 | 1 |
| 2 / 2 | 1 | 1 | 0 |
| 1 / 2 | 0.5 | 0 | 1 |
| Final: | 1010 |
Binary to Decimal process
A step-by-step breakdown on converting 1100 to decimal:
- Write down the binary number and identify each digit’s position
- Assign powers of 2 to each position
- Multiply each digit by its corresponding power of 2
- Add the products of all digits
| Position | Binary | Power of 2 | Calculation |
|---|---|---|---|
| 3 (leftmost) | 1 | 2^3 = 8 | 1 x 8 = 8 |
| 2 (Second) | 1 | 2^2 = 4 | 1 x 4 = 4 |
| 1 (third) | 0 | 2^1 = 2 | 0 x 2 = 0 |
| 0 (rightmost) | 0 | 2^0 = 1 | 0 x 1 = 0 |
| Final: | 12 |
Binary to Hexadecimal process
A step-by-step breakdown on converting 11010010 to hexadecimal:
- Group the binary digits into 4-bit chunks: 1101 0010
- Follow the binary to decimal process above
- Add all numbers from the calculation column
| Position | Binary | Power of 2 | Calculation |
|---|---|---|---|
| 3 (leftmost) | 1 | 2^3 = 8 | 1 x 8 = 8 |
| 2 (Second) | 1 | 2^2 = 4 | 1 x 4 = 4 |
| 1 (third) | 0 | 2^1 = 2 | 0 x 2 = 0 |
| 0 (rightmost) | 1 | 2^0 = 1 | 1 x 1 = 1 |
| Final: | 13 (D) |
| Position | Binary | Power of 2 | Calculation |
|---|---|---|---|
| 3 (leftmost) | 0 | 2^3 = 8 | 0 x 8 = 0 |
| 2 (Second) | 0 | 2^2 = 4 | 0 x 4 = 0 |
| 1 (third) | 1 | 2^1 = 2 | 1 x 2 = 2 |
| 0 (rightmost) | 0 | 2^0 = 1 | 0 x 1 = 0 |
| Final: | 2 |
The final result we got from both tables is D2.
Hexadecimal to Binary process
Remember, in a hexadecimal system, digits range from 0 to F, corresponding to decimal values 0 to 15.
A step-by-step breakdown on converting 3F to binary:
- Convert each hex digit to decimal - hex digits 0 - 9 are the same in decimal, while hex digits A to F correspond to decimal values 10 to 15.
- 3 in hex is 3 in decimal.
- F in hex is 15 in decimal.
- Follow the Binary to Decimal section above, and try to do it yourself:
- Convert 3 to binary, and we will get 0011.
- Convert 15 to binary and we will get 1111.
Bonus Tip: The table acts as a cheat sheet for binary, decimal, and hexadecimal conversion. No manual calculation is needed!
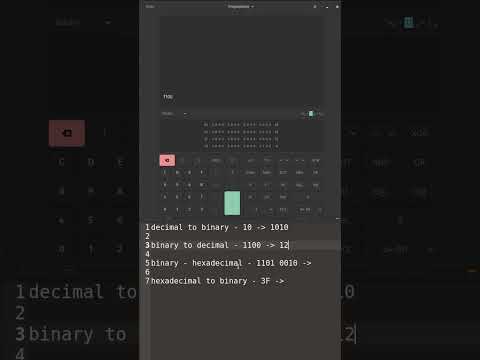
Alternative Way - Use Calculator
Open your calculator app and look for a “programmer” mode. This mode usually lets you see numbers in different formats, like decimal, binary, and hexadecimal.
Recap
Computers speak in numbers, but not the kind you’re used to. They rely on three main systems: decimal (0-9, our everyday numbers), binary (0s and 1s!), and hexadecimal (a mix of 0-9 and A-F). Binary is crucial because electronics use on (1) and off (0) states. Hexadecimal helps us write long binary strings in a more human-readable way.
By the way, if you’re curious about how binary numbers work and how they represent decimals, there’s a great website in the resources section (second link) that helped me understand it better. Check it out!
Resources
Decimal, Binary, and Hex conversion table by Educative
How Do Numerical Conversions Work in Computer Systems? Explained With Examples
Thank you!
Thank you for your time and for reading this!